Olá Marcelo, segue a dúvida:
Numa campanha de prevenção contra a dengue x pessoas dividiram igualmente entre si a tarefa de visitar 1000 casas de uma região da cidade. No dia previsto faltaram 5 pessoas e cada uma das outras pessoas teve de visitar 10 casas a mais. Qual é o número x de pessoas?
____________________________________________________________________________________________
Olá Natália,
Achei este exercício bem interessante, pois além de exigir do estudante a capacidade de interpretação do problema, envolve conceitos de sistemas lineares e equações do 2º grau.
Vou resolvê-lo passo a passo, para que ninguém fique com dúvidas.
Vamos à resolução.
____________________________________________________________________________________________
Primeiramente, vamos esquematizar nosso raciocínio de acordo com o que nos é fornecido no problema. Sendo x número de pessoas, e chamando de n o número de casas que cada pessoa visitou, temos:
- “... x pessoas dividiram igualmente entre si a tarefa de visitar 1000 casas de uma região da cidade..."
Ou seja, o número x de pessoas, vezes o número de casas que cada um visitou, será igual a 1000. Logo:
- “… faltaram 5 pessoas e cada uma das outras pessoas teve de visitar 10 casas a mais…”
Ou seja, o números x de pessoas menos 5, vezes o número de casas que cada um visitou mais 10, deve ser também igual a 1000. Assim:
Vamos agora desenvolver esta última equação.
Aplicando a propriedade distributiva:
Colocando n em evidência, e passando –50 para o outro lado:
Somando 1000 com 50, e passando 10x para o outro lado:
Passando (x-5) dividindo:
Agora vamos substituir a eq. II na eq. I, assim:
Multiplicando x pelo parênteses:
Passando (x-5) multiplicando:
Aplicando a propriedade distributiva:
Fazendo 1050x – 1000x, e passando –5000 para o outro lado:
Dividindo todos os termos por 10:
Onde, para o nosso problema, a = –1; b = 5; e c = 500.
Substituindo a, b e c na equação, fica:
Desenvolvendo:
Temos dois resultados possíveis para x. Um somando 45, e outro subtraindo. Chamarei estes resultados de x’ e x’’.
Encontrando x’:
Encontrando x’’:
Por fim, basta analisar qual das duas respostas se encaixa no nosso problema. Como o número de pessoas deve ser positivo, o valor que estamos procurando é x’’ = 25.
Portanto, o número x de pessoas é igual a 25.
Continue praticando, que é só com persistência que conseguimos sucesso não só em matemática, mas em tudo na vida.
Um abraço!
Marcelo Flora
____________________________________________________________________________________________
Saiba como enviar suas dúvidas. Clique aqui!




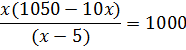
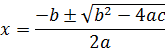
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhLY6dEDyA3BN13VN_qkCU3isGAUnvWDc2Mi2CXfKFA5fXUg0pDbo-vOUO2BkZ_KjubM_1kz2mbmHqSx8Hu6ZEBEovLOlV7hDDyAOiy0sTyX2eqvXFI_3ook5tZcnEeWko9zXZ3oNJX-Do_/?imgmax=800)
![clip_image004[5] clip_image004[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhAVSkcB_iXKJYOyLGoVQAtQO5PT2OHk7xmU-BzkGA8lLGeCX5fB1Tv8riBuEoRkfTTHqK-OSfBlvF-7n4af9aXqozq5FYdgErJ4BIr0QqnZMlGb-sWgCLhR_ZpcKHjV1tT3djXEvV0G2uZ/?imgmax=800)
Olá Marcelo; Ótima resolução! Abraços!
ResponderExcluirpor favor ,como resolver essa questões
ResponderExcluir1) faap-sp calcular x se log 1000x - log(0,001)x=1
2)para que valores de x temos log1/2 (x+2)2= log1/2 36?
4)(ita-sp)log2 16-log4 32 é igual a:
a) y = log2 (x+4)
b)y = log(-3x9)10